线性代数

Linear Algebra

第一部分

\begin{aligned} A x & = b \end{aligned}

矩阵乘以向量的三个理解层次：

First level: Only numbers 只有数字的运算
Second level: combination of column vectors 列向量的线性组合
Third level: Subspace 子空间的运算

线性方程组
 向量
 矩阵
 逆矩阵

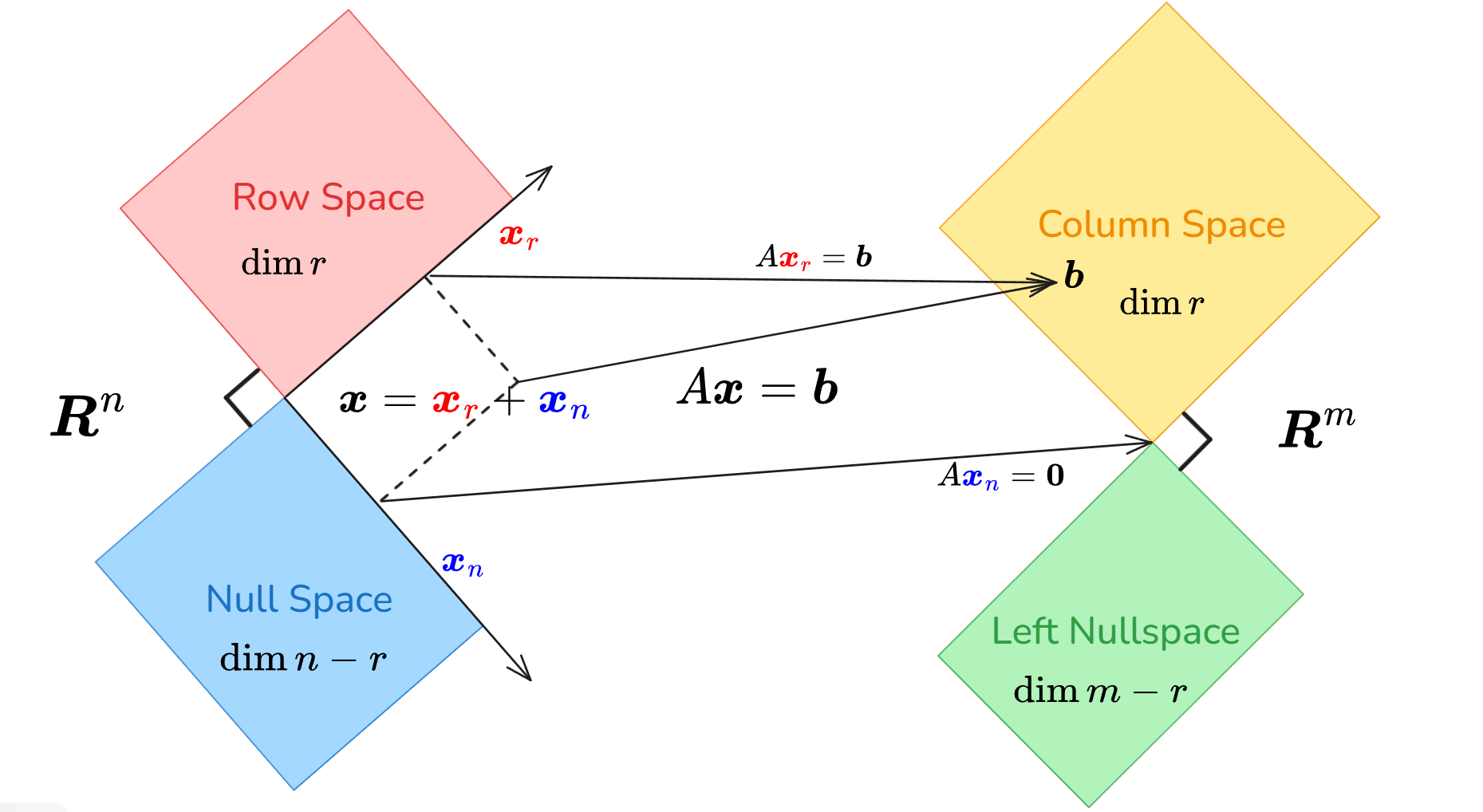
矩阵的初等变换
 矩阵的秩
 线性方程组的解
 行列式
 克拉默法则
 雅可比矩阵

向量空间范数
 线性变换线性独立
 正交性标准正交基子空间的正交性
 向量投影

第二部分

\begin{array}{r} A x = λ x \end{array}

特征值和特征向量
 对称矩阵
 矩阵对角化
 二次型

微分方程组
 凯莱-哈密顿定理
 矩阵求导
 奇异值分解

矩阵分解

Matrix Factorizations

矩阵分解	所属知识点
$A = L D U$	线性方程组的解	用于求解线性方程组、求逆、行列式计算
$A = Q R$	标准正交基	最小二乘法、求正交基、特征值计算
$A = X Λ X^{- 1}$	矩阵对角化	解微分方程、稳定性分析、幂法计算特征值
$S = Q Λ Q^{T}$	对称矩阵	泛用于 PCA（主成分分析）、谱图理论、物理系统对角化
$A = B J B^{- 1}$	Jordan矩阵	理论分析
$A = U Σ V^{T}$	奇异值分解	图像压缩、降维、主成分分析（PCA）等
$A = Q S$	极分解	量子力学、信号处理、图像分析
$A = U Λ U^{- 1}$	正规矩阵	简化线性算子分析，常用于量子力学
$A = Q T Q^{- 1}$	Schur分解	广泛用于特征值算法
$S = C^{T} C$	Cholesky分解	快速求解正定线性系统

$L$ $C$ Lower triangular
$D$ Diagonal
$U$ $C^{T}$ Upper triangular
$X$ Eigenvectors
$Λ$ Eigenvalues
$B$ Generalized Eigenvectors
$J$ Jordan
$Q$ $V$ $U$ Orthogonal
$Σ$ Singular Value

相关概念

图论
 坐标变换

参考资料

Gilbert Strang.Introduction to Linear Algebra. Fifth Edition 清华大学出版社